開關轉換器之回授控制‒OTA Type II/III之相位提升
摘要
Type II 補償器通常用於電流模式控制的開關轉換器回授電路,一般可獲得良好的線電壓與負載調節及暫態響應。然而當工作點(如輸入電壓或負載電流)改變,原設計的補償器可能會有穩定度變差,或相位裕度不足的情形發生。此外,當轉換器的工作環境發生變化,如溫度、濕度、或零件老化等,都可能造成系統穩定度的改變,甚至導致電源系統不穩定。本文探討因應原設計參數改變而採用相位提升電路,以改善系統穩定度,並以立錡科技降壓轉換器RT2857B為實例說明穩定度改變的情形,提出兩種相位提升電路作為改善,最後以Mathcad作計算及SIMPLIS作電路模擬,驗證理論的分析。
一、降壓型轉換器之小信號模型
探討電源轉換器的回授設計首先須從功率電路的開環轉移函數開始;其頻率響應是非線性的,透過小信號模型而線性化後,可以獲得隨工作點而異的轉移函數。根據此開環的轉移函數來設計回授補償電路,使閉環路系統具有低的線電壓及負載調節率,且對於負載電流瞬變發生時,輸出電壓可有很低的過衝(overshoot)與很快的回復穩態的調節時間(settling time);此外,也希望能對環境溫度、長時間老化等都有相當的因應能力。而評價閉環效能並達到上述之目標最簡單的方法就是透過電源系統的環路增益(loop gain)分析,並藉由交越頻率與相位裕度以比較系統的響應頻寬與相對穩定度。
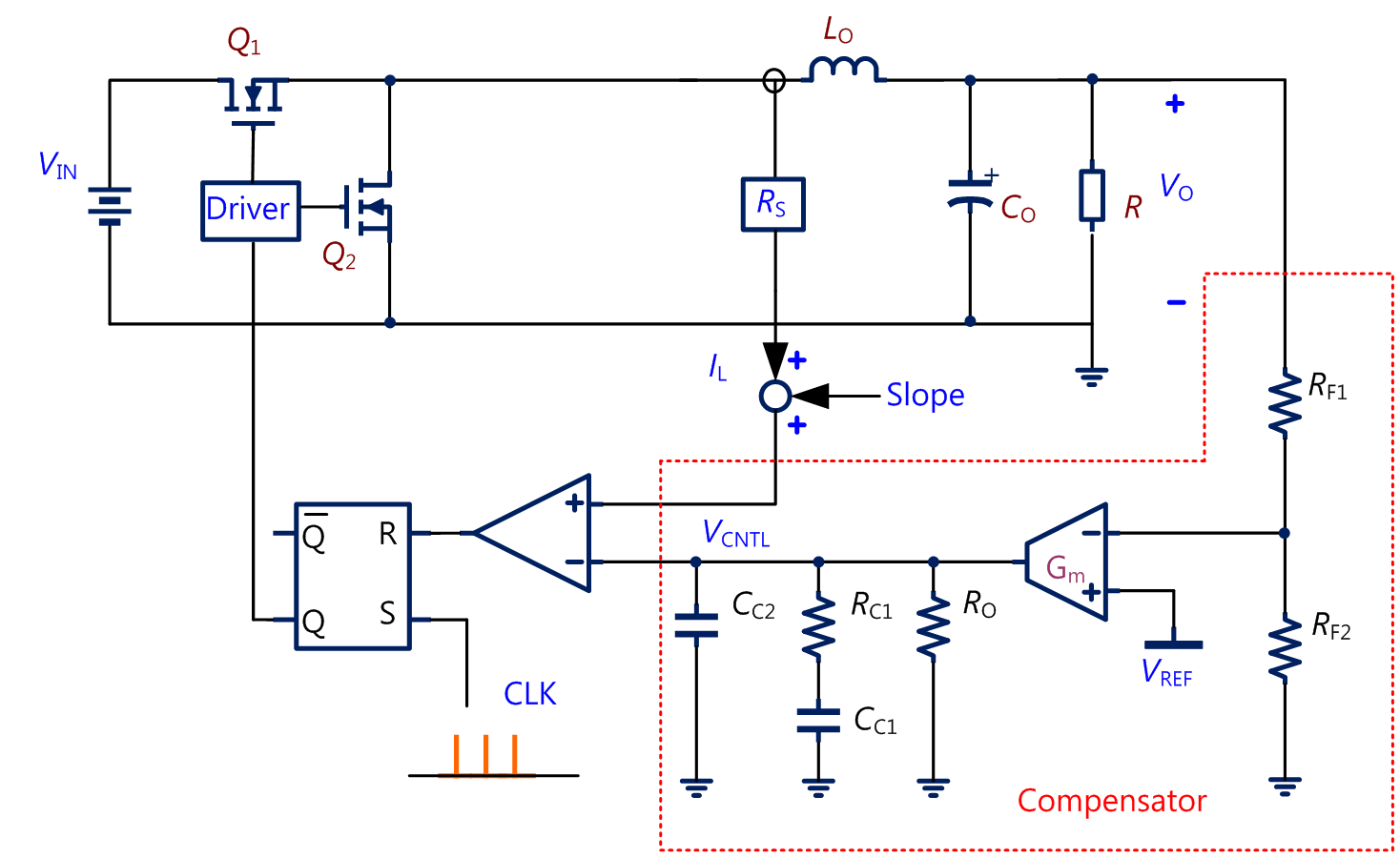
圖 1、降壓型開關轉換器電路與其回授電路
圖1為一常規峰值電流控制(peak current mode control)的降壓型轉換器電路,紅色虛線區域為其回授補償電路(compensator)。輸出電壓VO經RF1、RF2分壓採樣,與一參考電壓VREF作比較,其誤差經過放大之後,得到一控制電壓VCNTL;控制電壓再與經電感電流檢知增益RS之電感電流峰值比較得到控制開關晶體Q1的邏輯信號,完成雙環閉迴路控制。
功率電路的開迴路轉移函數,即從控制電壓VCNTL到輸出電壓VO的頻率響應,本文採用的是雙環控制(two-loop feedback)降壓轉換器小信號模型,其模型演進與推導相當繁複,不是本文的重點,詳細的電路模型與參數推導可參考文獻[1,2,3]。此功率電路在連續導通模式(continuous conduction mode)下的開環轉移函數可由以下近似式式(1)表示:
 (1)
(1)
其中,
 (2)
(2)
 (3)
(3)
 (4)
(4)
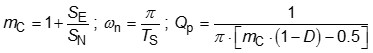 (5)
(5)
在式(1)中,直流增益除了與工作點R、D有關外,也和電感電流檢知增益RS、電感值LO、開關周期TS以及斜坡補償(SE,SN)有關係,相當複雜。其中Fp(s)有一個低頻的極點ωp以及輸出電容ESR零點。如式(4)所示,ωp與工作點、輸出濾波器LO、CO,以及斜坡補償有關,即當工作點變化時,ωp極點也會隨之而變;分子為輸出電容ESR零點,並不會隨工作點改變。Fh(s)為採樣維持函數的近似值;在開關頻率一半的地方有兩個極點,同時有一個與補償斜坡有關的Qp值。從式(5)可知,當其分母趨近於0時,Qp值會變很大,即形成一個尖峰(peaking),此尖峰會造成次諧波振盪(subharmonic oscillation)。若工作週期D高於0.5且無斜坡補償(mC=1)時,Qp值為負值,表示Fh(s)在一半開關頻率時會有一對共扼複數極點,相位會陡降,而增益大小則有一尖峰,造成系統不穩定。解決方法是加入斜坡補償SE,讓Qp為正值,以確保系統穩定。(SN電感電流的上升斜坡量。)
為方便以數值說明,本文後續都採用立錡科技RT2857B電流模式控制同步整流降壓轉換器之功率電路當成回授設計的受控平台。其開關頻率設定為420kHz,內嵌固定斜坡補償量SE =54 mV /μs;電感電流檢知增益RS為62mV/A。輸入電壓範圍為6V至12V,輸出電壓為1.8V,最大負載電流為6A。功率電感選用2.2μH,其繞線電阻為11mΩ;輸出電容330μF,其等效串聯電阻(ESR)為9mΩ。
圖2為應用立錡RT2857B降壓型轉換器在各種不同輸入電壓與負載電流條件下之增益曲線,其中輸出電壓VO均為1.8V,而四條曲線分別代表高壓輕載(VIN=12V,IO=0.6A)、低壓輕載(VIN=6V,IO=0.6A)、高壓重載(VIN=12V,IO=6A)以及低壓重載(VIN=6V,IO=6A)等四個工作條件。如圖所示,因為峰值電流控制有輸入前饋的作用,輸入電壓對增益的影響不大。此範例將先以高壓重載條件(VIN=12V,IO=6A)設計,如前所述,若選定一工作點進行補償器設計,為避免相同的補償器應用於其他條件如高壓輕載時(VIN=12V,IO=0.6A),補償效果受到影響,仍須檢查其他條件下的相位裕度(phase margin),以確保系統的穩定。
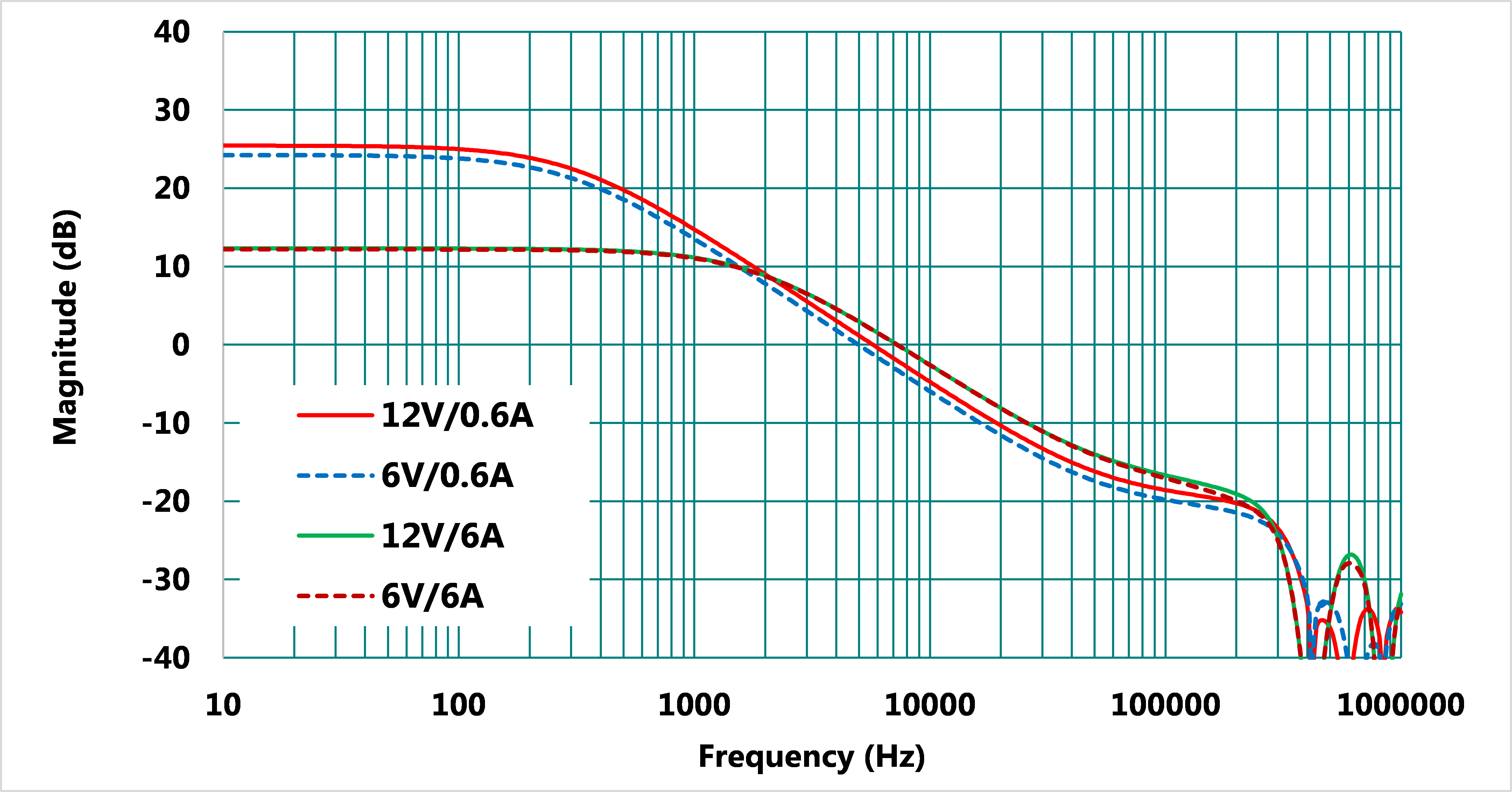
圖 2、不同輸入輸出條件下之控制電壓對輸出電壓的增益曲線
圖3為輸入電壓VIN=12V,負載電流IO=6A 的工作點下,依式(1)所得之頻率響應波德圖,包括增益及相位。其低頻直流增益為12dB;在745Hz處有一個極點fP1,53kHz有一輸出電容ESR零點fZ1,在一半開關頻率,約210kHz處,有一對共軛複數極點fP2、fP3,增益與相位陡降,分別以-40dB/dec和‒180°/dec之斜率衰減。
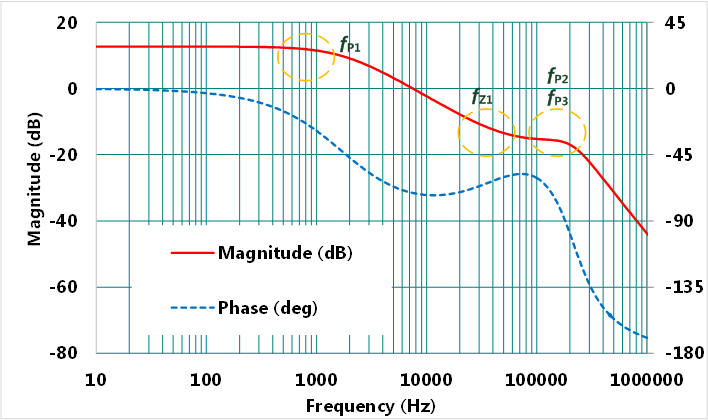
圖 3、功率級轉移函數波德圖(VIN = 12V,IO = 6A)
所謂環路增益(loop gain)是功率電路的頻響增益與補償電路增益的乘積。對一個電源轉換器而言,若要有很低的線電壓與負載穩壓率,在零頻率時,要有很高的環路增益,所以一般補償器在零頻率會有一個極點。另外,為了系統穩定,以及兼顧暫態響應(transient response),環路增益的單位增益頻寬(unit-gain bandwidth),也就是通稱的交越頻率(crossover frequency),會設計在大約開關頻率(fS)的1/20 到1/5之間;且必須有相當程度的相位裕度,最好是在50°以上。有了上述之系統需求,就可以設計補償器了。
本文是以最為熟知與採用的極零點置放法(pole-zero placement)作補償器設計。以峰值電流模式控制的降壓轉換器為例設計補償器時,除上述之零頻率極點外,並在功率電路的低頻極點處fP1置放一個補償器零點fCZ1;在中頻輸出電容ESR零點處fZ1置放一個補償器極點fCP1;如此,加上適當的直流增益設計,環路增益便可以-20 dB/dec 的直線通過所設定的交越頻率點。至於在功率電路高頻段的雙極點,因為頻率已經遠高於交越頻率,增益低於0dB,通常在設計補償器時不會考慮。
簡單的說,補償器會有一個零頻率極點,及一個低頻的零點,到了電容ESR處有一個極點。這樣的補償器,通稱為Type II補償器。一般峰值電流模式控制的降壓轉換器若採用Type II補償器,都可得到滿意的效能。然而當電源系統的工作點改變,或交越頻率設定的不適當,或是電路器件的參數值(特別是電容)因為老化而變質等等,都會讓原來的閉環系統穩定度受到影響,相位裕度降低。下章將從回授補償器的組態探討,以找到簡單方便的解決方案。
二、OTA Type II 與 Type III補償器的設計
運算跨導放大器(Operational Transconductance Amplifier;OTA)之功能為將輸入差分電壓(differential voltage)轉換為 輸出電流訊號,可視為一電壓控制電流源(Voltage-Controlled Current-Source;VCCS)。相對於運算放大器(Operational Amplifier;OPA),OTA的結構較簡單,在IC內部比較容易實現,且沒有「虛擬接地」(virtual ground),所以在電源控制IC中,常作為回授控制之誤差放大器。因此,本文主要探討如何利用OTA實現較常使用的Type II與Type III補償器,且如前所述,以高壓重載為設計補償器之工作點。
圖4(a)為OTA之內部等效電路模型,而圖4(b)為其電路符號。正端VIN+與負端VIN-的電壓差為其輸入信號,乘上OTA之跨導Gm,即為其等效之輸出電流信號。此電流源並聯一高輸出阻抗RO與一雜散輸出電容CO,即得到OTA 的輸出電壓。Gm與RO的乘積即為其開環路直流電壓增益,通常可高達60dB以上;RO與CO造成的極點,決定了OTA的開路頻寬,可達數MHz以上。
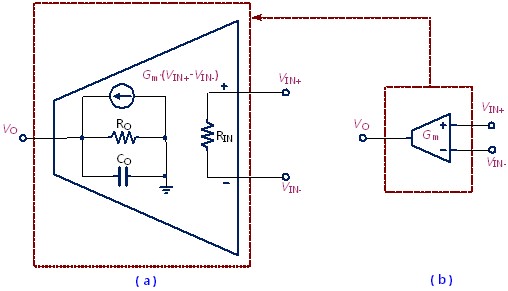
圖 4、OTA電路(a)OTA等效模型(b)OTA電路符號
1.
OTA Type II補償器
式(2)為一標準Type II補償器轉移函數,具有一零點ωCZ1與二個極點:零頻率極點及ωCP1,A為直流增益大小,圖5為其對應之波德圖。
 (2)
(2)
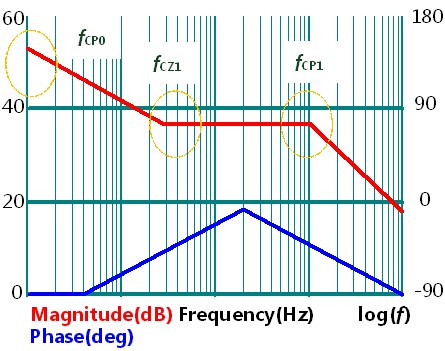
圖 5、Type II補償器增益與相位之波德圖
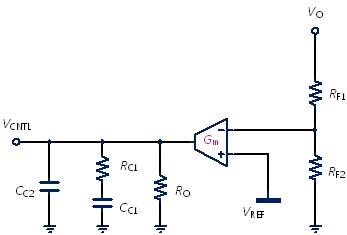
圖 6、OTA之Type II補償器
圖6所示為一OTA Type II補償器,推導其轉移函數結果,如式(3),
 (3)
(3)
比較式(3)與式(2),二者有相同形式,列出fCZ1與fCP1及A公式如下:
 (4)
(4)
 (5)
(5)
 (6)
(6)
此補償器有一零頻率的極點,一個零點fCZ1,一個極點fCP1,本文採用極零點放置法,fCZ1與fCP1分別對應於功率級745Hz的極點與53KHz的ESR零點。如前所述交越頻率決定後,將其代入可算出補償器在交越頻率下的相對應的增益,並算出A,以確定補償器的所有係數。
極零點放置法的目標是讓電路的閉環路增益以-20dB/dec斜率通過所設計的交越頻率。如此設計補償電路,僅能確定所需的交越頻率,但相位的部份則無法保證。若所得之相位裕度無法滿足系統需求,就必須降低交越頻率的設定,或是採用更高階次的補償器。圖7為所設計出之OTA Type II補償器,使用Mathcad之理論計算的環路增益。
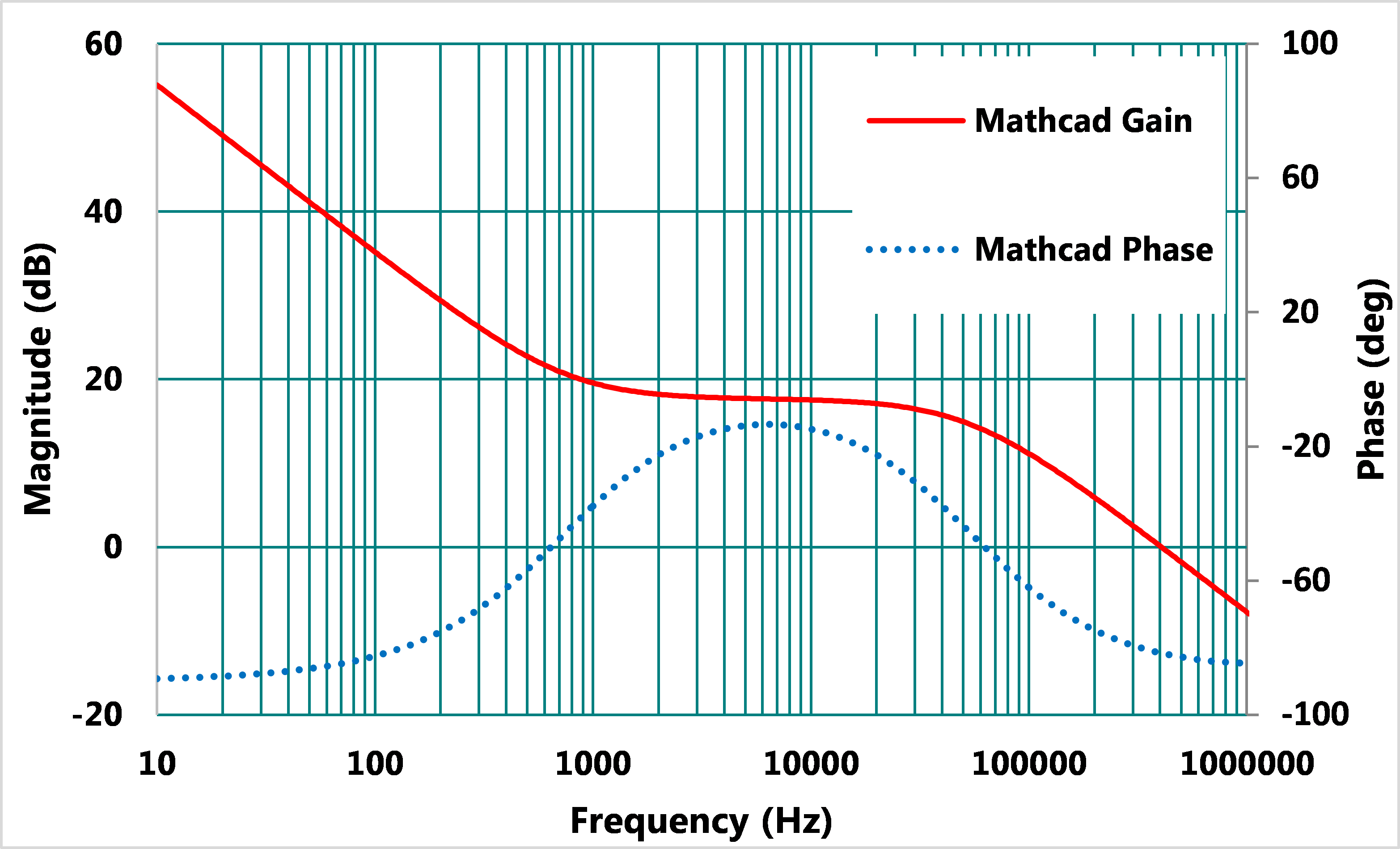
圖7、Type II補償器增益與相位之波德圖
2.
Type III補償器 – Type II加相位提升電容
如上所述,若所得之相位裕度無法滿足系統需求,除降低交越頻率的設定之外,亦可採用更高階次的補償器。在原本的Type II補償器中先加入一個零點fCZ2與再加入一個極點fCP2,相位在新加的極零點頻率之間得到了提升,且可維持原本設計的交越頻率。
圖8,在原本的OTA Type II補償器電路之上方分壓電阻上並聯一個電容CF1,在相位上會增加一個零點與極點,以提高相位裕度,此電容通稱為相位提升器(phase booster)或又稱為前饋電容(feedforward capacitor)。加了此相位提升電容之後,即為三極點二零點(three-pole two-zero;3P2Z)的補償器,也是一種Type III補償器。
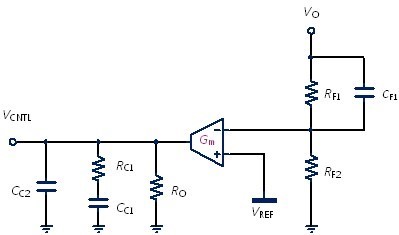
圖8、Type III補償器 – Type II加相位提升電容
推導圖8轉移函數如式(7),
 (7)
(7)
 (8)
(8)
 (9)
(9)
 (10)
(10)
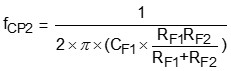 (11)
(11)
 (12)
(12)
由式(10)、(11)可以看出,新增的零點fCZ2與極點fCP2是和CF1、RF1以及RF2有關,而RF1和RF2關係被輸出電壓與參考電壓的比值固定,因此,新增的零點和極點存在著一相依的關係,在設計零點時,極點也就被決定了。雖設計的自由度受限,但若小心調試也可達到相位提升的效果。圖9為Type II加上相位提升電容的補償器,用Mathcad計算的理論環路增益。
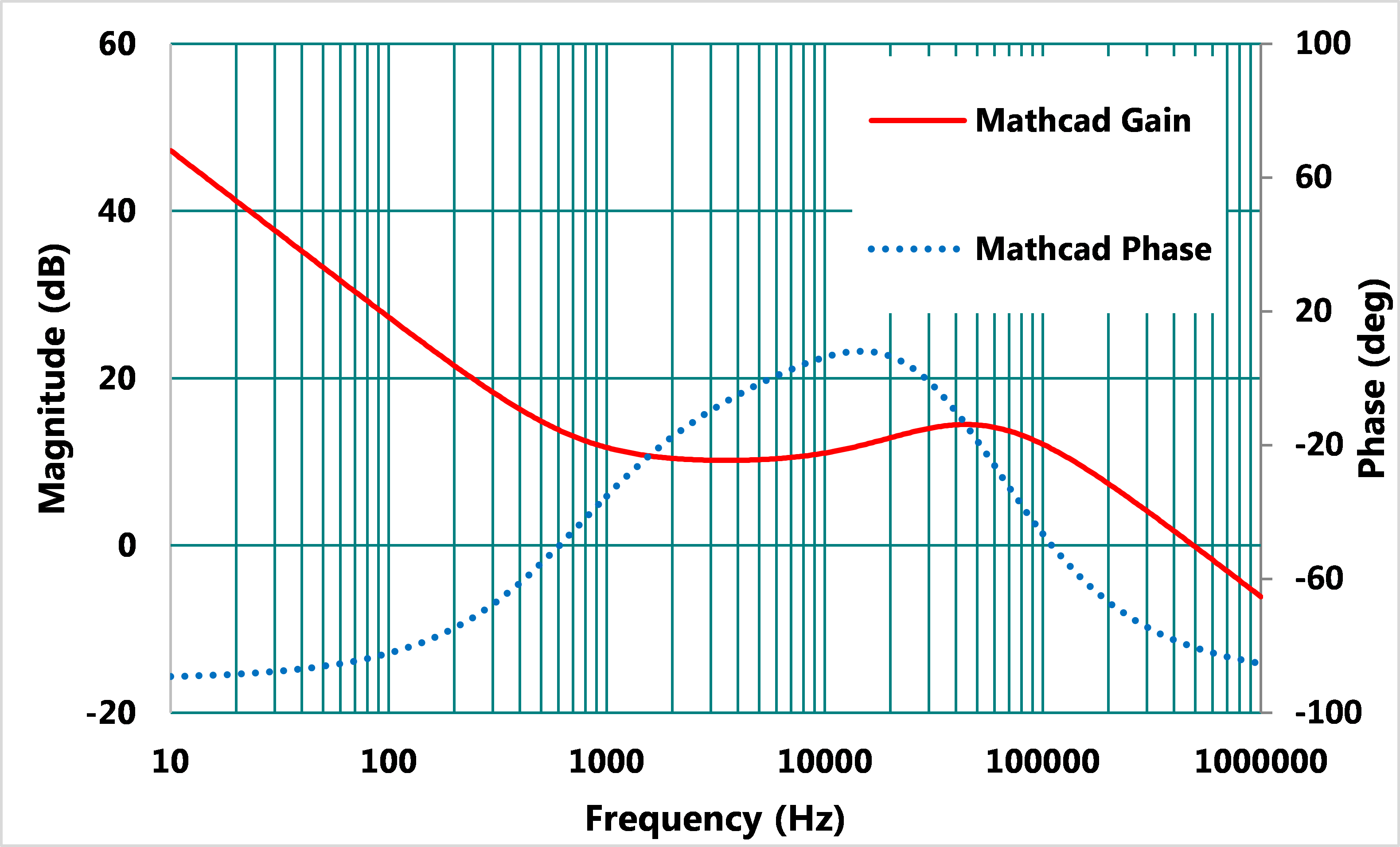
圖9、Type II加相位提升電容之補償器增益與相位之波德圖
3.
Type III補償器 – Type II加相位提升電容與電阻
上述之Type II補償器,只能確保交越頻率,無法保證足夠的相位;若使用Type II加相位提升電容的補償器,則有設計自由度不夠的問題。因為新增加的極點fCP2與零點fCZ2相依,其相依關係等於輸出電壓與參考電壓的比值,若輸出電壓為3.3V,參考電壓為0.6V,極點頻率就為零點頻率的5.5倍,且固定無法調整,應用上受到限制。
改善方法可如圖10,在原本的OTA Type II補償器電路之上方分壓電阻上並聯一組電容與電阻,依然會增加一個零點與極點,亦為三極點二零點(three-pole two-zero;3P2Z)的Type III補償器。
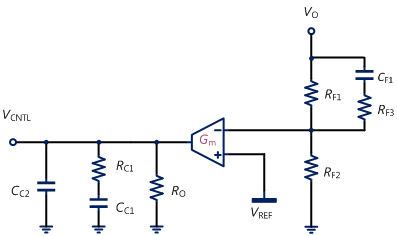
圖10、Type III補償器 – Type II加相位提升電容與電阻
推導其轉移函數如式(13),
 (13)
(13)
 (14)
(14)
 (15)
(15)
 (16)
(16)
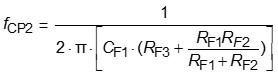 (17)
(17)
(18)
由式(16)、(17)可以看出,新增的零點fCZ2與極點fCP2是和CF1、RF1、RF2以及RF3有關,RF3可調整fCZ2與fCP2的相對位置,增加設計的自由度。圖11為所設計出之OTA Type II加上相位提升電容與電阻的補償器,使用Mathcad計算的理論環路增益。
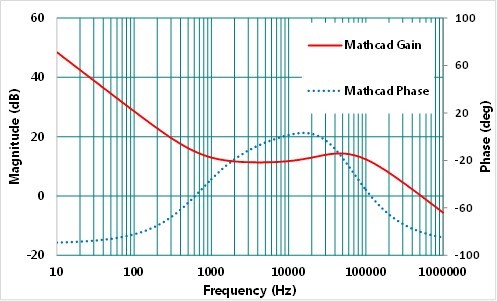
圖11、Type II加相位提升電容之補償器增益與相位之波德圖
三、設計範例
本章將以實例來說明上述之補償器設計方法。以第一章提到的功率電路平台參數進行討論,並使用圖3之相關極零點參數,依序說明Type II、Type II加相位提升電容、與Type II加相位提升電容電阻的二種Type III補償器之設計程序。利用上述之所推導之關係式可算出補償器之各電路元件參數,將參數代入模擬平台SIMPLIS驗證與理論計算作比較,並可觀察各補償器對系統閉迴路相位提升之效果。
1.
Type II補償器
設定交越頻率為60kHz。通常是選擇開關頻率的1/5到1/20,此範例開關頻率為420kHz,60kHz為1/7的開關頻率。
1. 已知降壓轉換器極點fP1=745Hz、ESR零點fZ1=53.59kHz,採用極零點對消法,設計補償器零極點與之對消,即fCZ1 = fP1 =745Hz ,fCP1= fZ1=53.59 kHz。
2. 由式(1),可得功率級在交越頻率下之增益為-14dB。將fCZ1,fCP1代入式(2),可得補償器在交越頻率時,增益下降76.9 dB。因此補償器之係數A須補償此二衰減的增益,使閉迴路增益在交越頻率下為0dB。因此A=91.073dB,或還原其倍數,即為35800。
3. 因設計考量及通用性,可選擇RF1 = 10kΩ。已知系統參數VO=1.8V,轉換器參數VREF=0.6V,由其電路關係VO/VREF=(RF1+RF2)/RF2,可得RF2=5kΩ。
4. 已知Gm為1.3mA/V,A=35800,將RF1,RF2代入式(6),可得CC1+ CC2=12nF。
5. 將fCZ1=745Hz,fCP1=53.59kHz及CC1+ CC2=12nF代入式(4)、(5),可得CC2=168pF,CC1=11.934nF。
6. 將CC1=11.934nF及fCZ1=745Hz代入式(4),可RC1=17.9kΩ。
上述設計程序已求得所有Type II補償器的電路參數,將其代入Mathcad作計算並用SIMPLIS作模擬,其結果如圖12,13,相位裕度為66°。
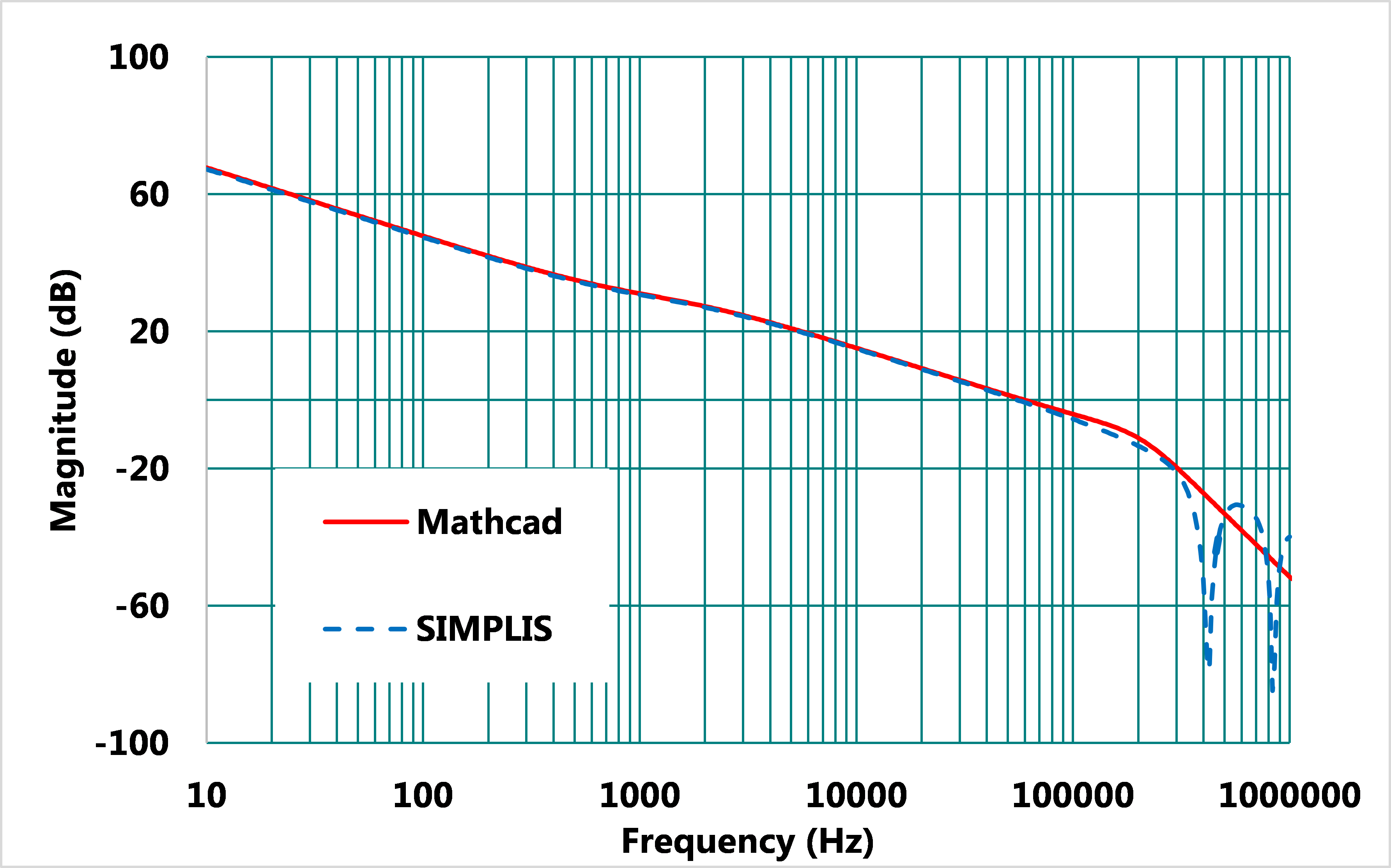
圖12、使用Type II 補償器之閉迴路增益曲線波德圖
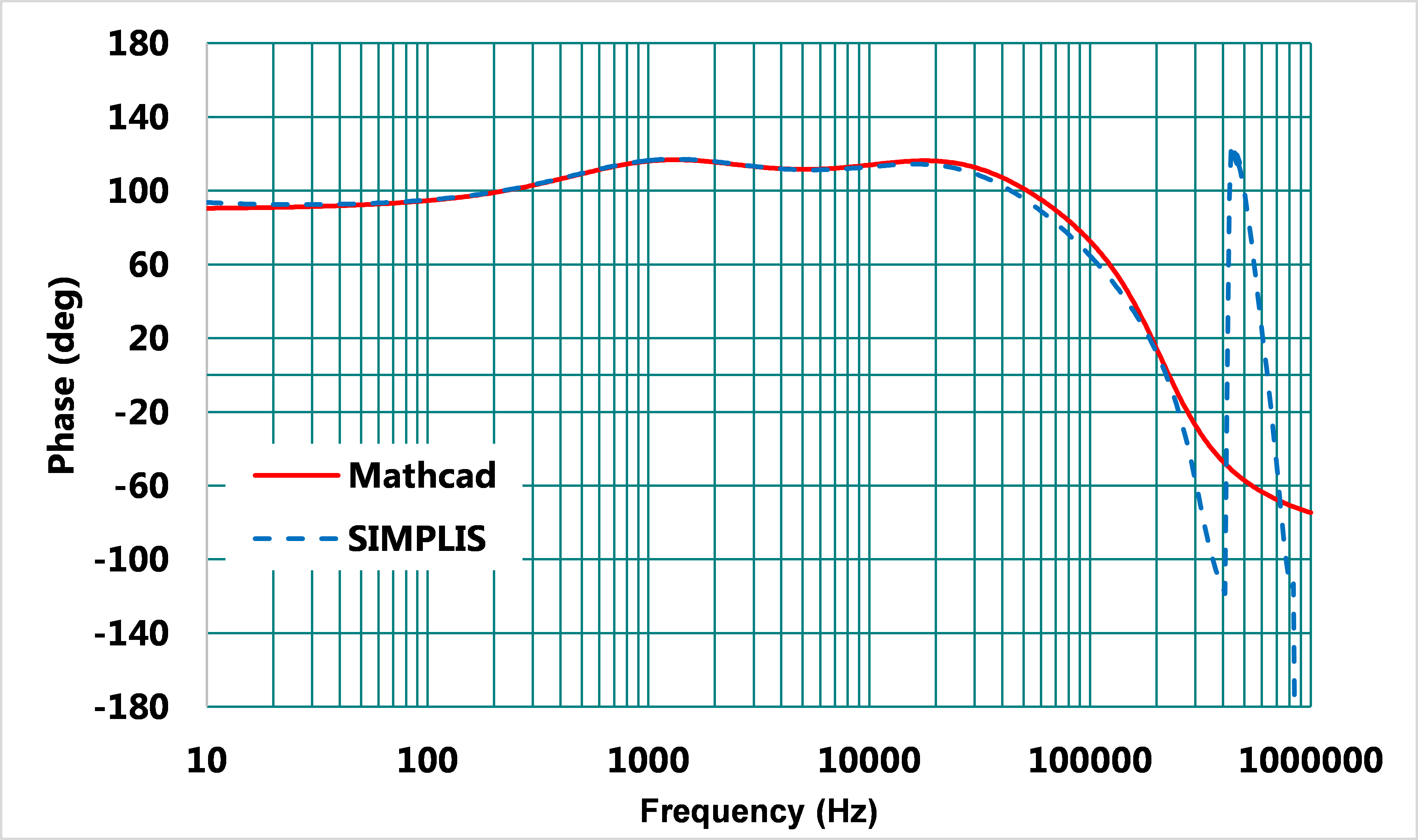
圖13、使用Type II 補償器之閉迴路相位曲線波德圖
2. Type II補償器考慮元件老化
在實際應用上,相位裕度為66°已有不錯的穩定度,但電路元件在高溫或是長時間工作之下,內部化學反應以及漏電流導致介質電壓降低,可能出現老化的情況而造成參數誤差變化,如輸出電容的容值變小與等效電阻變大等,閉迴路的特性因此改變,以下範例討論上述的狀況。
輸出電容值(CO)330μF 衰減至 160μF。等效電阻(ESR)9mΩ 增加至 12 mΩ。當以上參數改變,根據式(2)、式(4)可知功率級的fP1與fZ1會跟著變化,fP1變更為1.53kHz,fZ1變更為82.89kHz,功率級的極零點會往後偏移,若使用相同的Type II補償器,因為fZ1零點位置延後,可預見交越頻率會提高,相位裕度也會因為接近雙極點而衰減。
電容老化的範例,使用同樣的Type II補償器,閉迴路補償結果改變,其模擬與計算結果如圖14、15,交越頻率為90kHz,相位裕度降為41°,相位大幅減少,在元件老化時,原本良好的系統穩定性會受到影響。
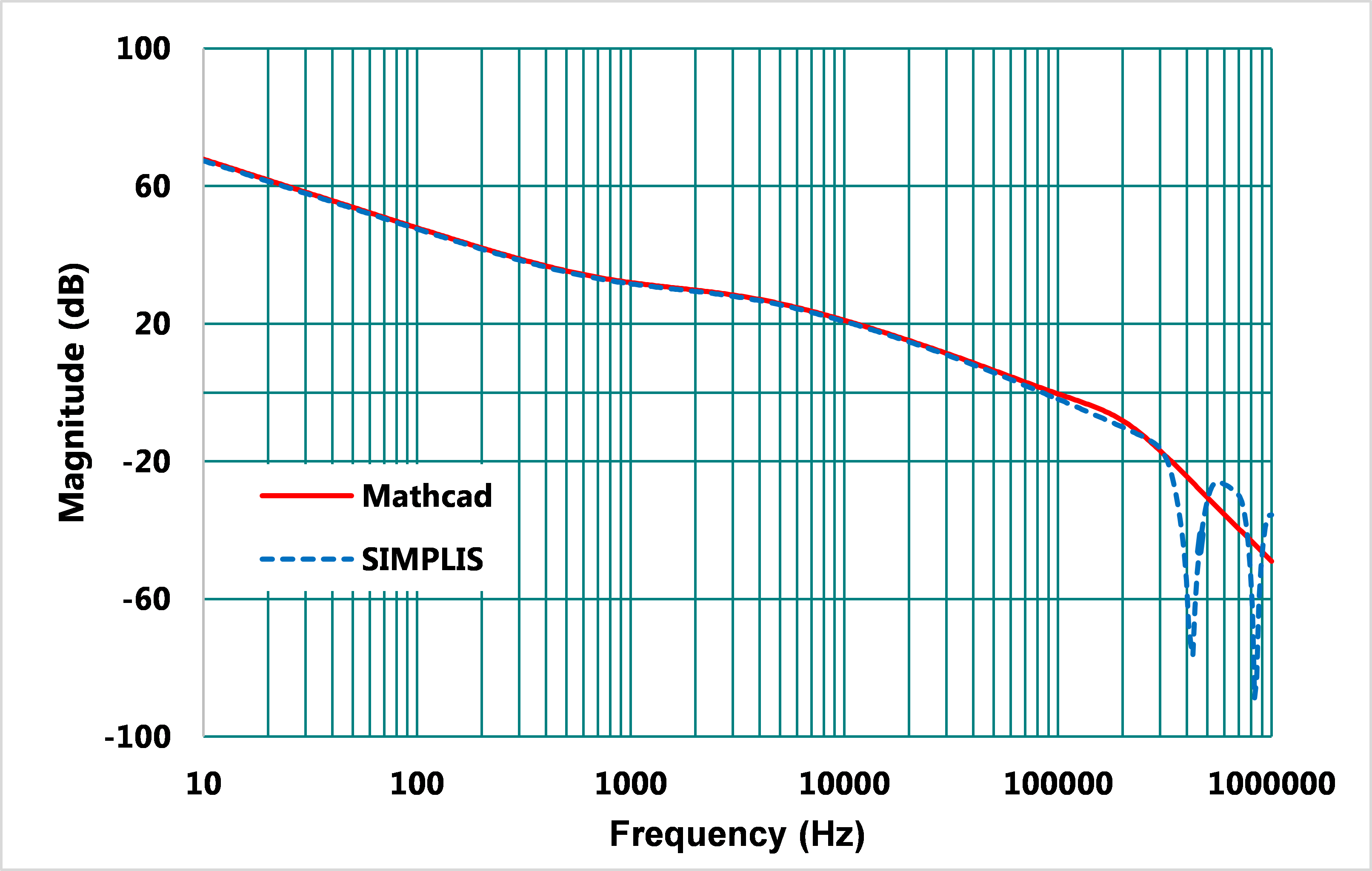
圖14、使用Type II 補償器之閉迴路增益曲線波德圖(輸出電容老化)
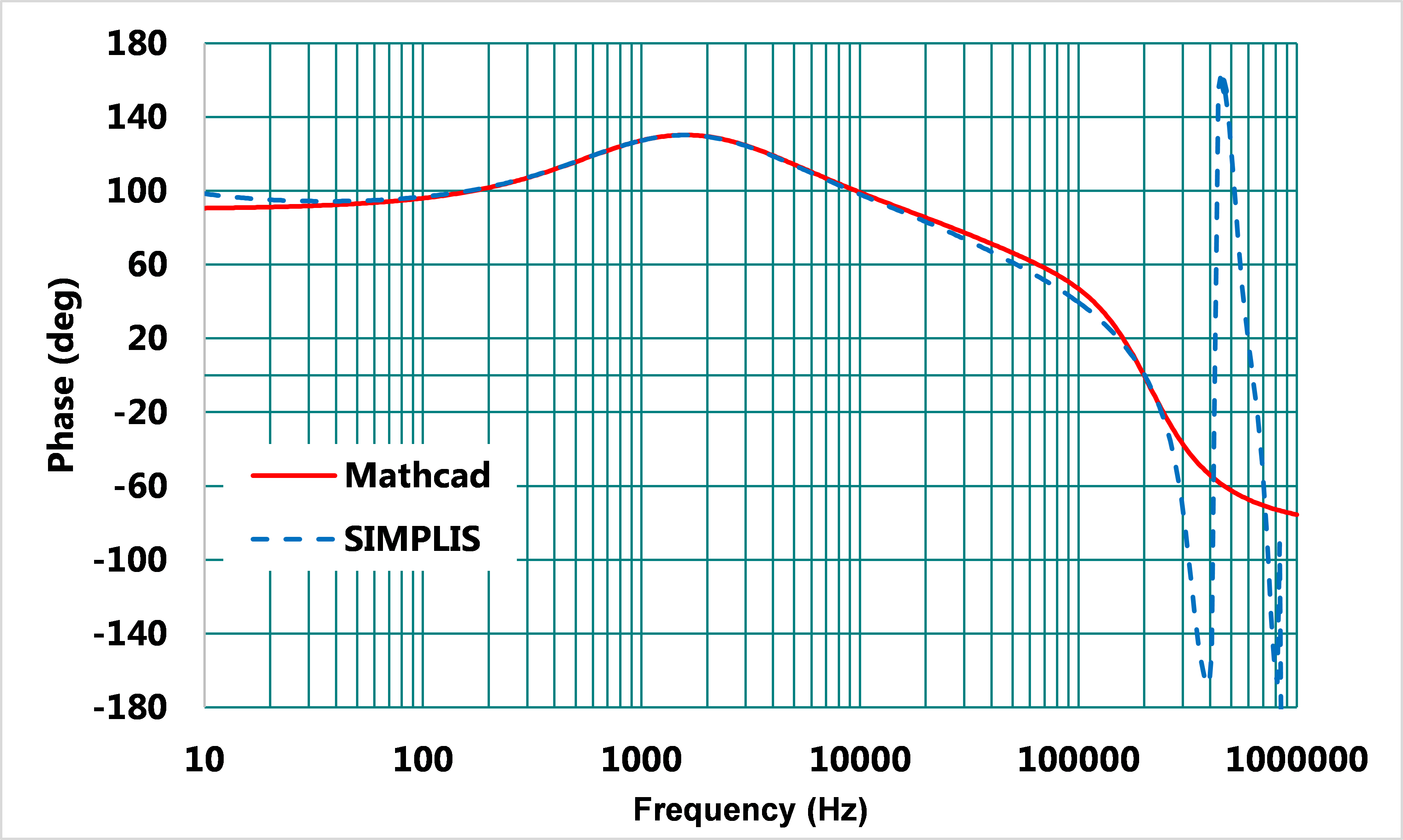
圖15、使用Type II 補償器之閉迴路相位曲線波德圖 (輸出電容老化)
3. Type III補償器 – Type II加相位提升電容
使用Type II增加相位電容進行設計,目標提高閉迴路的相位裕度,先決定新的補償器零點頻率fCZ2=20 kHz,因二者之相依關係,可得極點頻率fCP2=60 kHz。依照前述設計流程,得出相關參數:
RF1 = 10kΩ,RF2=5kΩ,CC1=26.7nF,CC2=376pF,RC1=8kΩ,CF1=795pF
將上述求得所有Type II補償器及相位提升電容的電路參數(以上設計程序雖只示範一組,但可自行調試),將其代入Mathcad作計算並用SIMPLIS作模擬,其結果如圖16,17,相位裕度大為改善,從66°提升到92°,但是新增的補償器極零點仍為相依關係,無法決定個別位置。
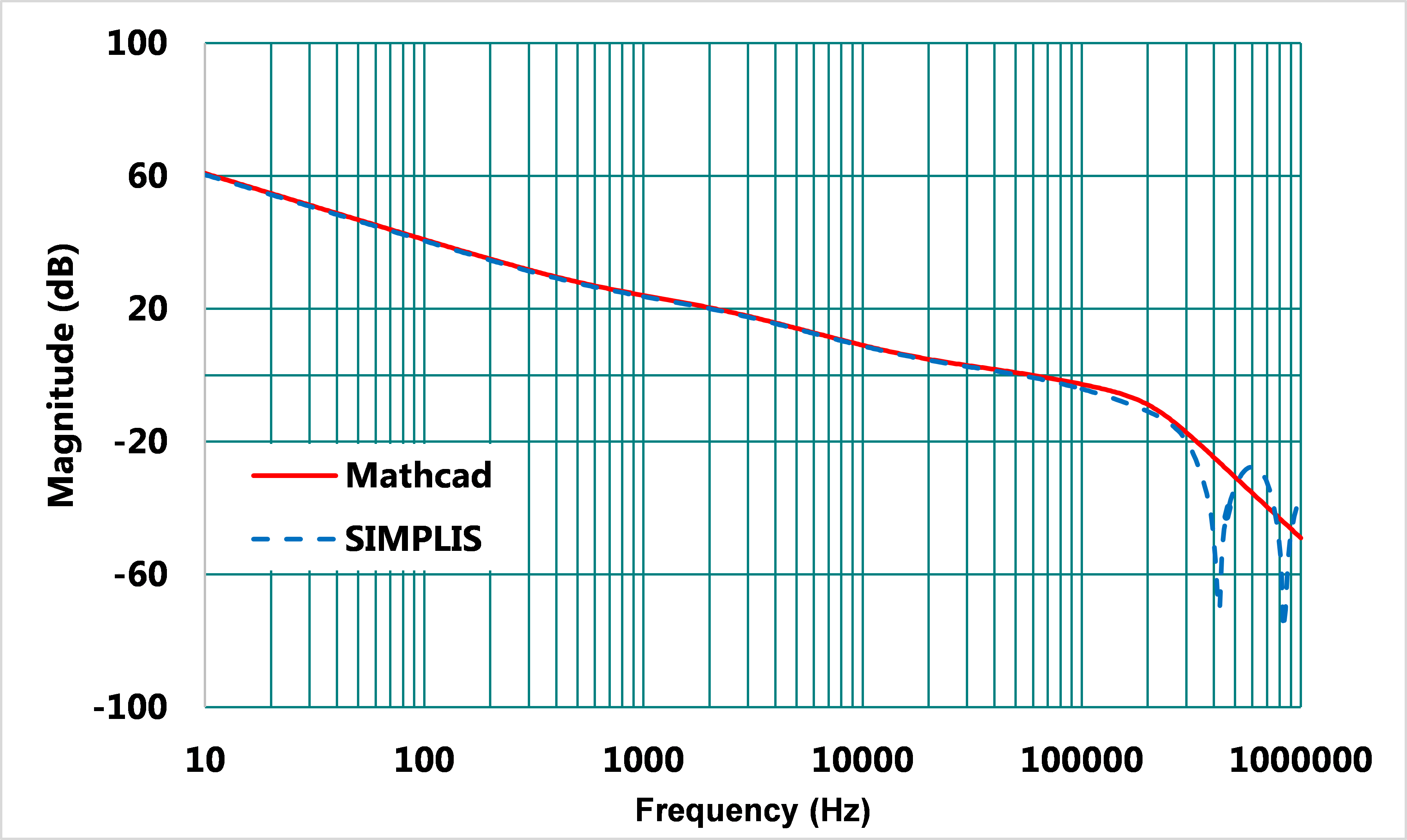
圖16、閉迴路增益曲線波德圖
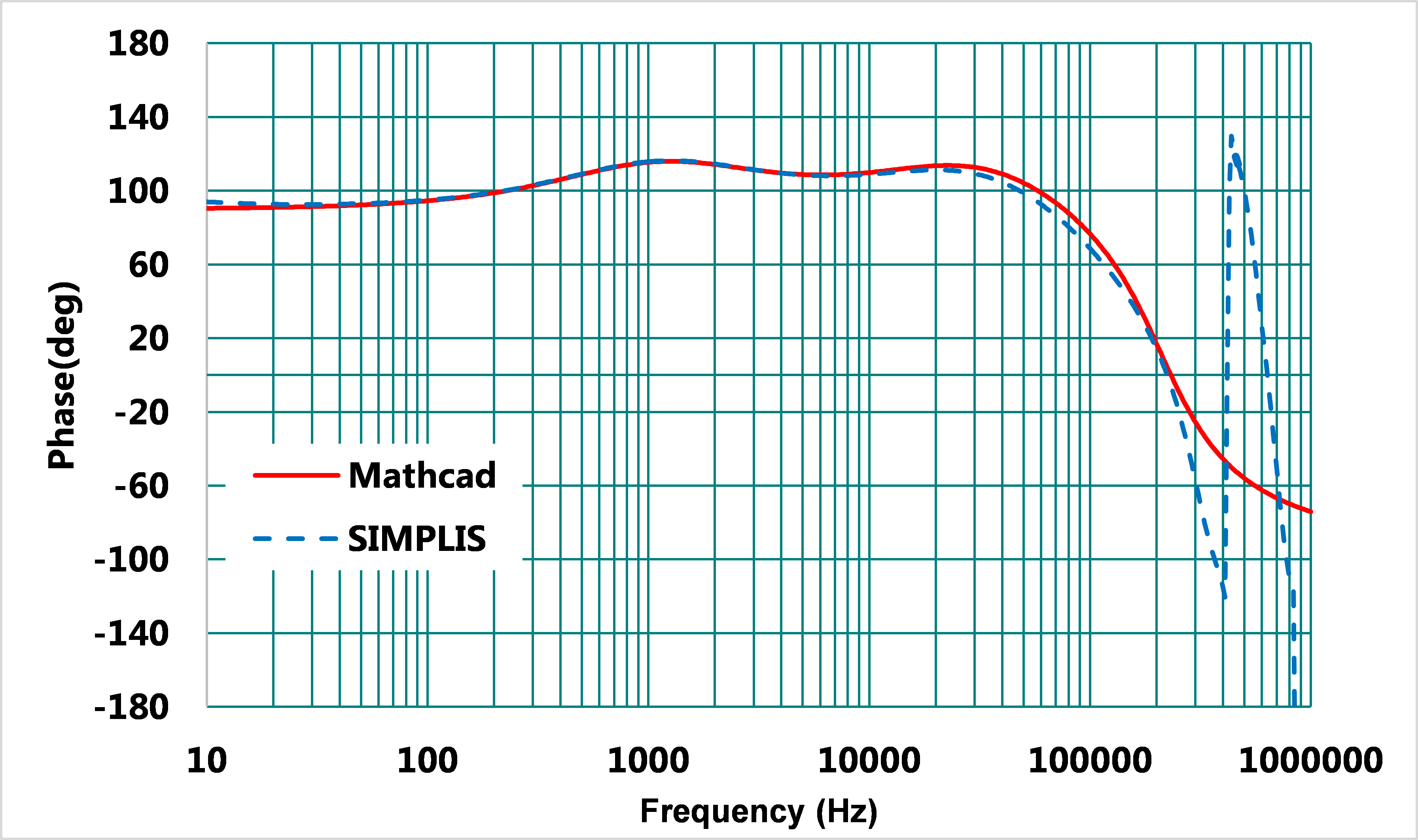
圖17、閉迴路相位曲線波德圖
4. Type III補償器 – Type II加相位提升電容 考慮元件老化
考慮相同的元件老化條件,使用Type II補償器加相位提升電容,進行閉迴路補償,其模擬與計算結果如圖18、19,交越頻率為90kHz,相位裕度為64°,可以看出,在元件老化等極端條件下,使用相位提升電容的補償器結果,相位裕度仍能維持在64°,因應外在不確定因素的影響,保持好的系統穩定性 。
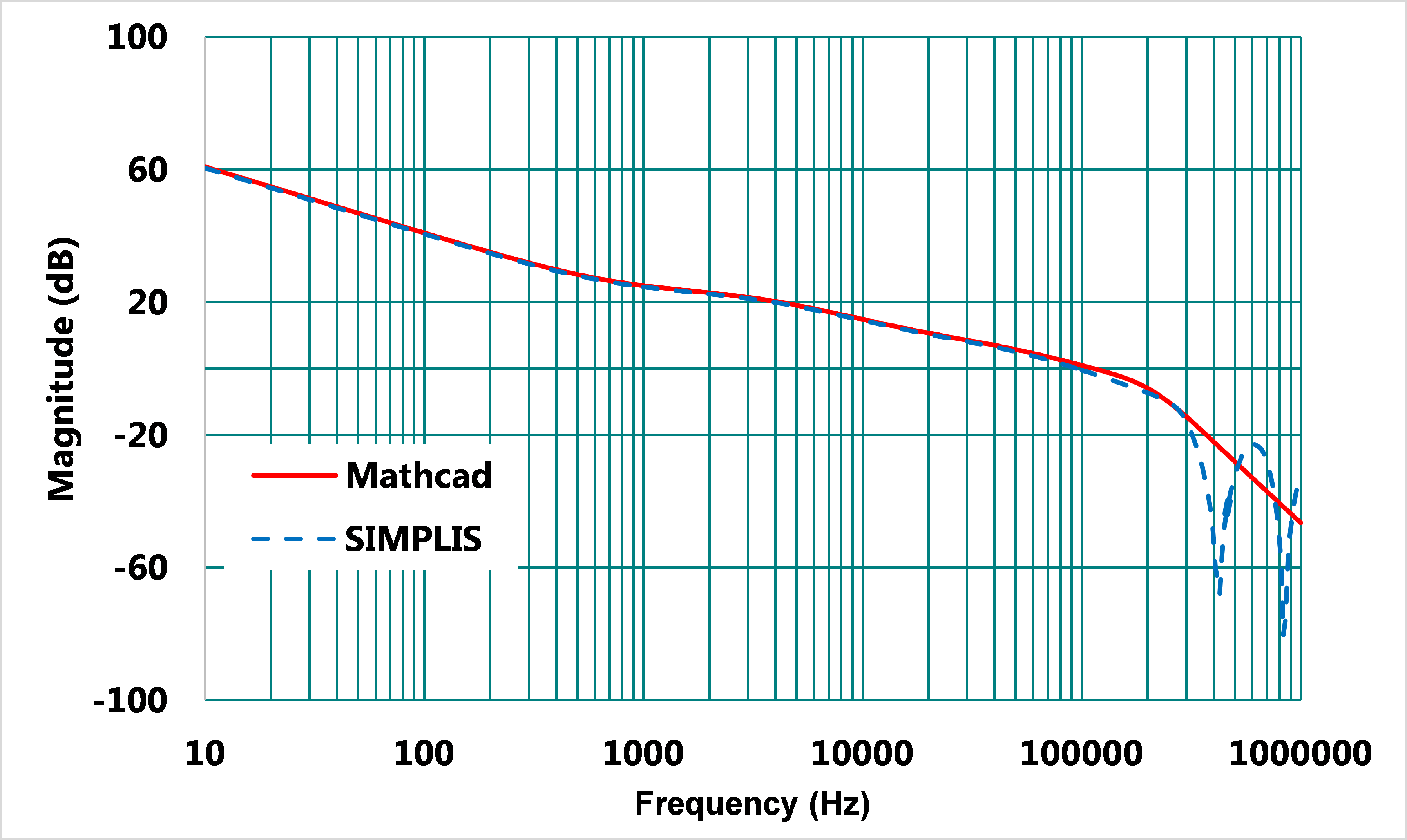
圖18、使用Type III 補償器之閉迴路增益曲線波德圖(輸出電容老化)
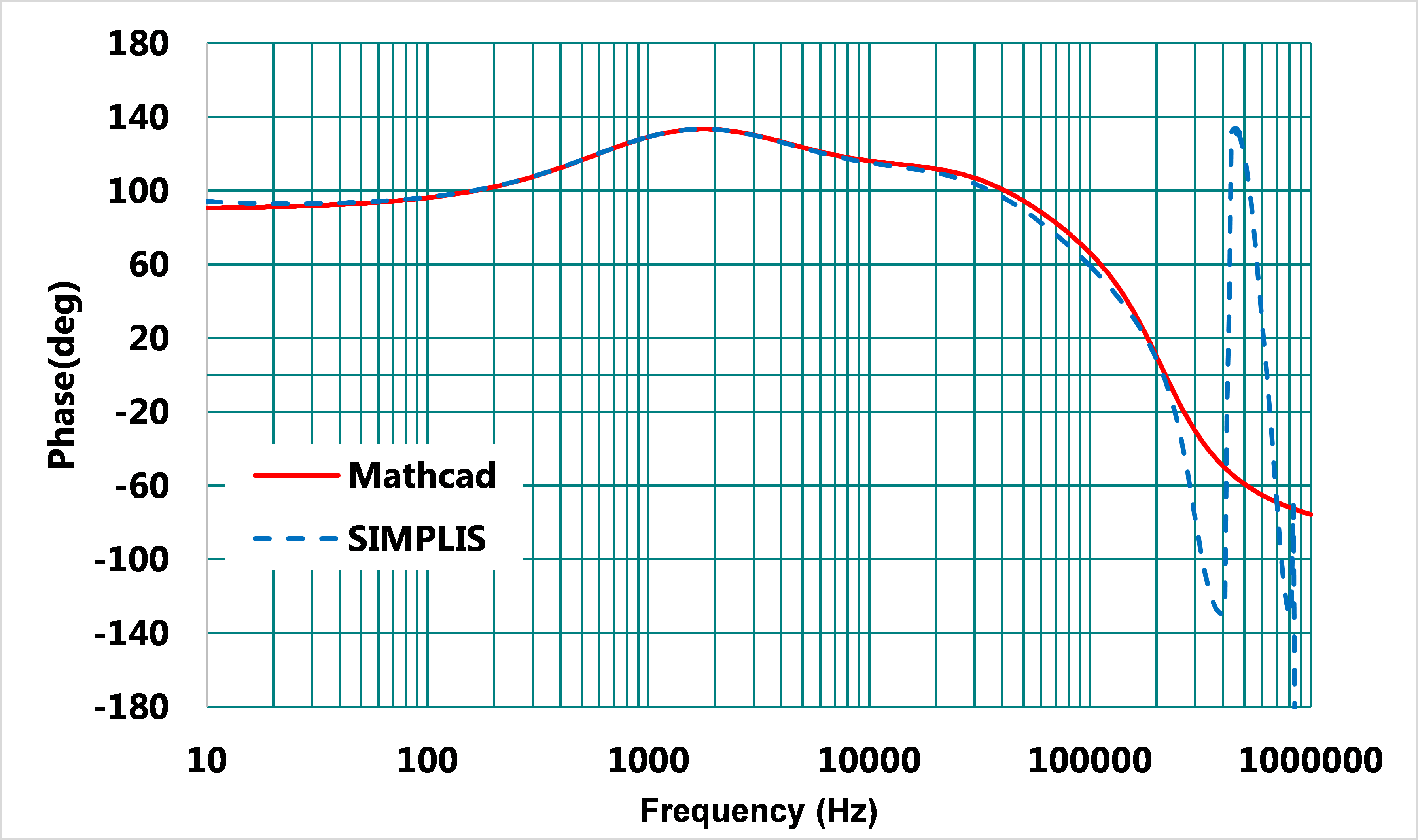
圖19、使用Type III 補償器之閉迴路相位曲線波德圖(輸出電容老化)
5. Type III補償器 – Type II加相位提升電容與電阻
討論Type II加相位提升電容與電阻的設計自由度。此範例功率級參數改變,工作條件為輸入電壓VIN 12V、輸出電壓變更為常用的VO 3.3V。
首先以Type II加相位提升電容進行設計,因為輸出電壓改變,且極零點與電壓VO及參考電壓VREF比值一致,所以補償器fCZ2與fCP2的倍率為5.5倍。設計fCZ2=20kHz,會自動決定fCP2=110kHz。
相關設計參數如下:
RF1=10kΩ,RF2=2.22kΩ,CF1=795pF,CC2=263pF,CC1=44.642nF,RC1=11.3kΩ。
模擬與計算結果如圖20,21,交越頻率仍為60kHz,因為新增零點與極點距離為5.5倍,fCP2頻率更往後,導致相位較晚衰減,所以閉迴路相位提升到112°,但過大的相位,也可能會造成系統的震盪,此時希望降低極點fCP2頻率到最佳的工作點,但在此範例中,因使用"Type II加相位提升電容的補償器",其極零點有相依性的緣故,將無法做任何設計變動,設計自由受限。為了改善此問題,可以增加電阻,提高設計自由度。以下進行Type II加相位提升電容與電阻的設計。
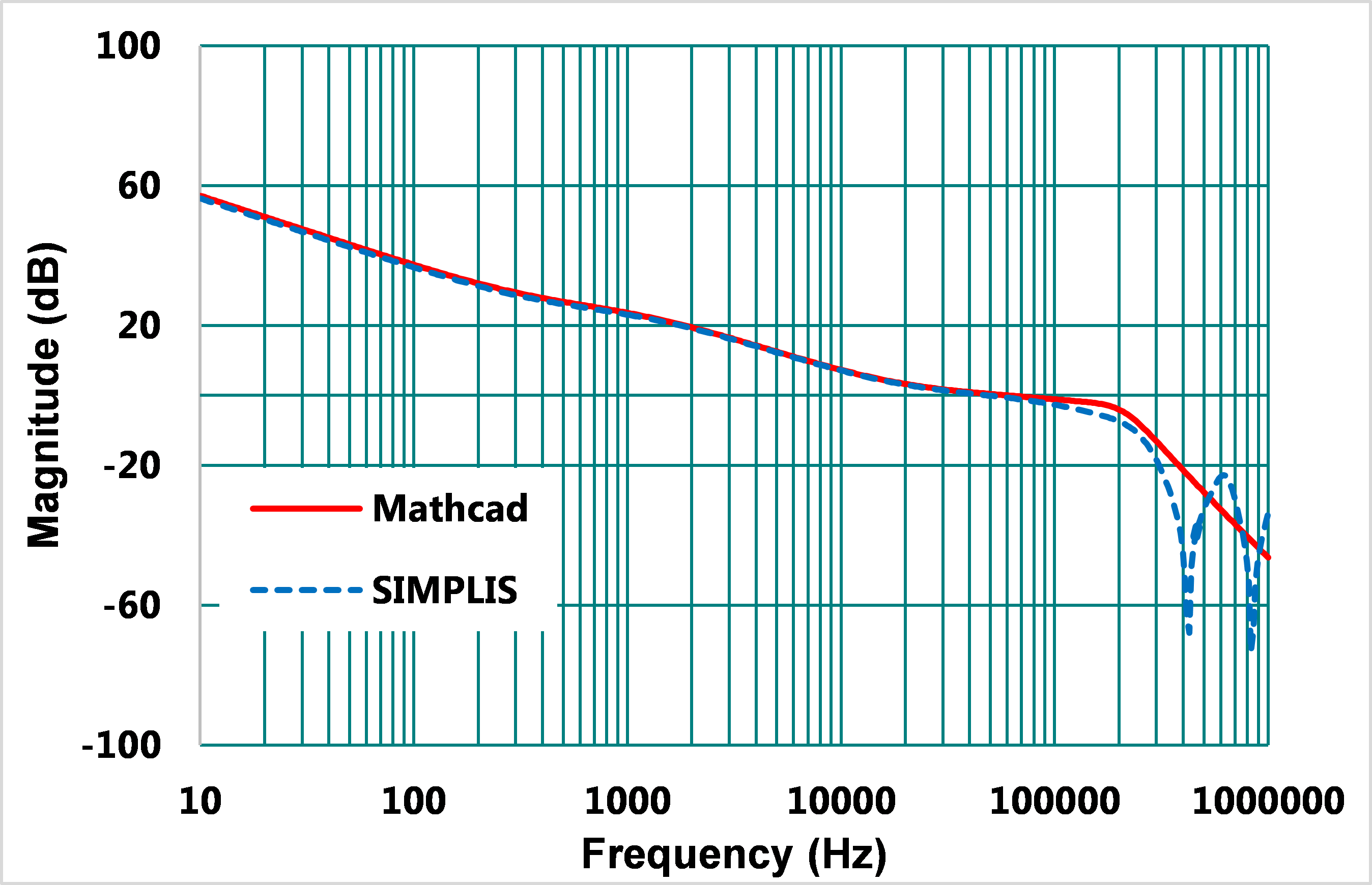
圖20、閉迴路增益曲線波德圖
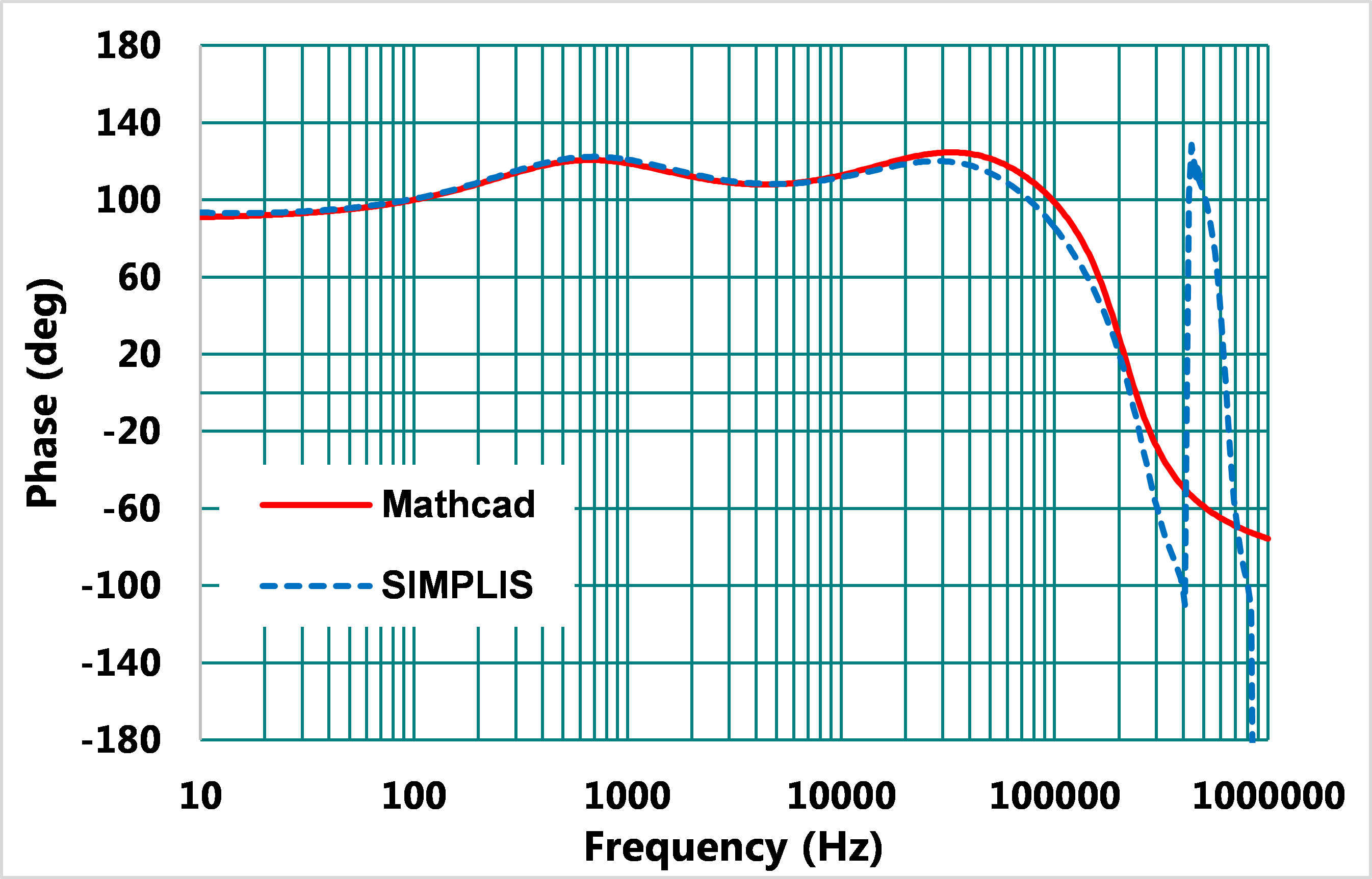
圖21、閉迴路相位曲線波德圖
增加相位電容電阻進行設計,目標縮短新增極零點的距離,先決定新的補償器零點頻率fCZ2=20 kHz,以及極點頻率fCP2=40 kHz。依照前述設計流程,可得出相關參數:
RF1=10kΩ,RF2=2.22kΩ,CC1=28.207nF,CC2=166pF,RC1=17.9kΩ,CF1=486pF,RF3=6.36kΩ
新的極點fCP2、零點fCZ2倍率因為電阻RF3的參與,可以從最大固定的5.5倍調整到2倍,其結果如圖22,23,交越頻率仍為60kHz,相位也依照使用者設計需求到達85°的目標。
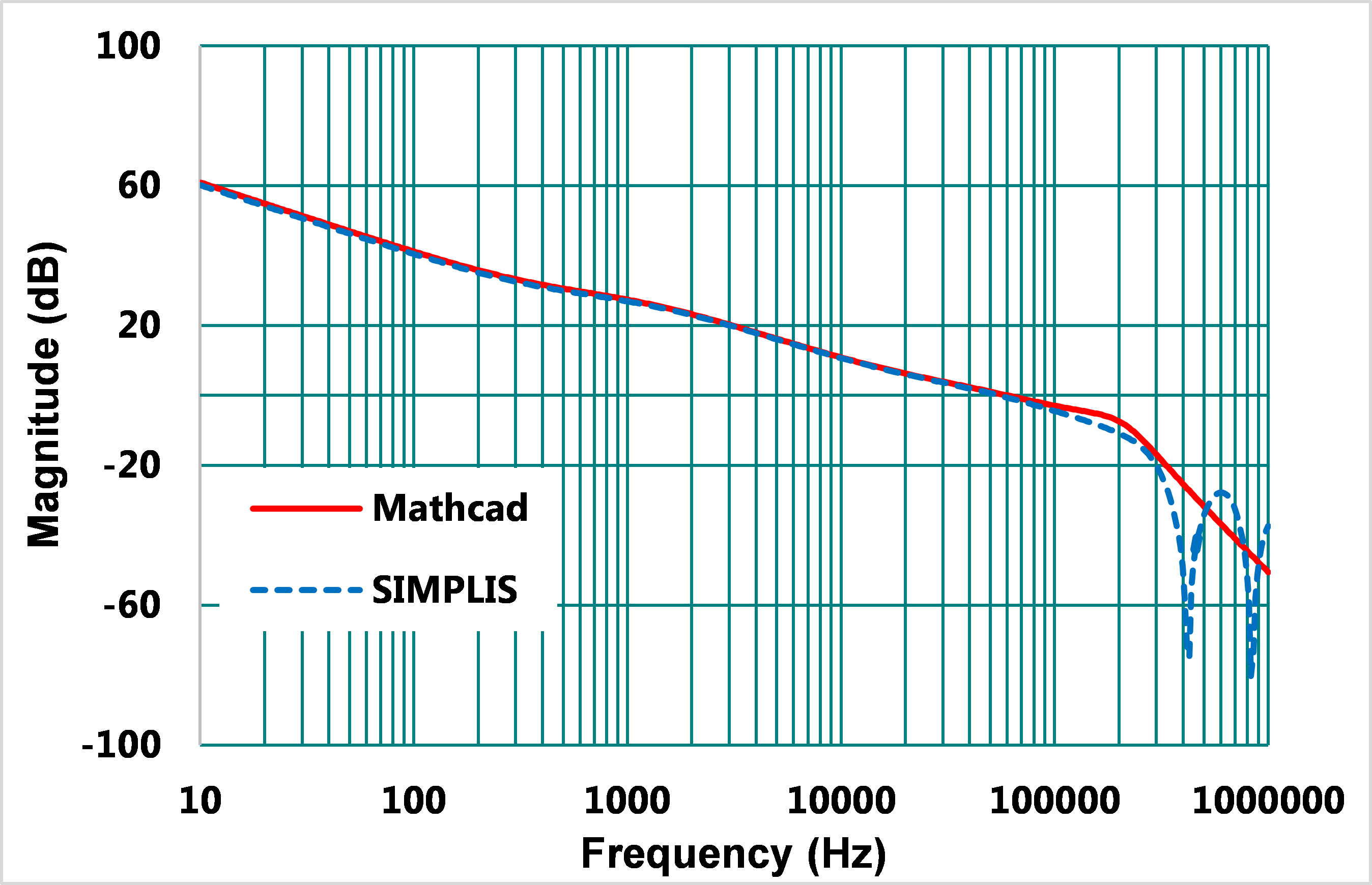
圖22、閉迴路增益曲線波德圖
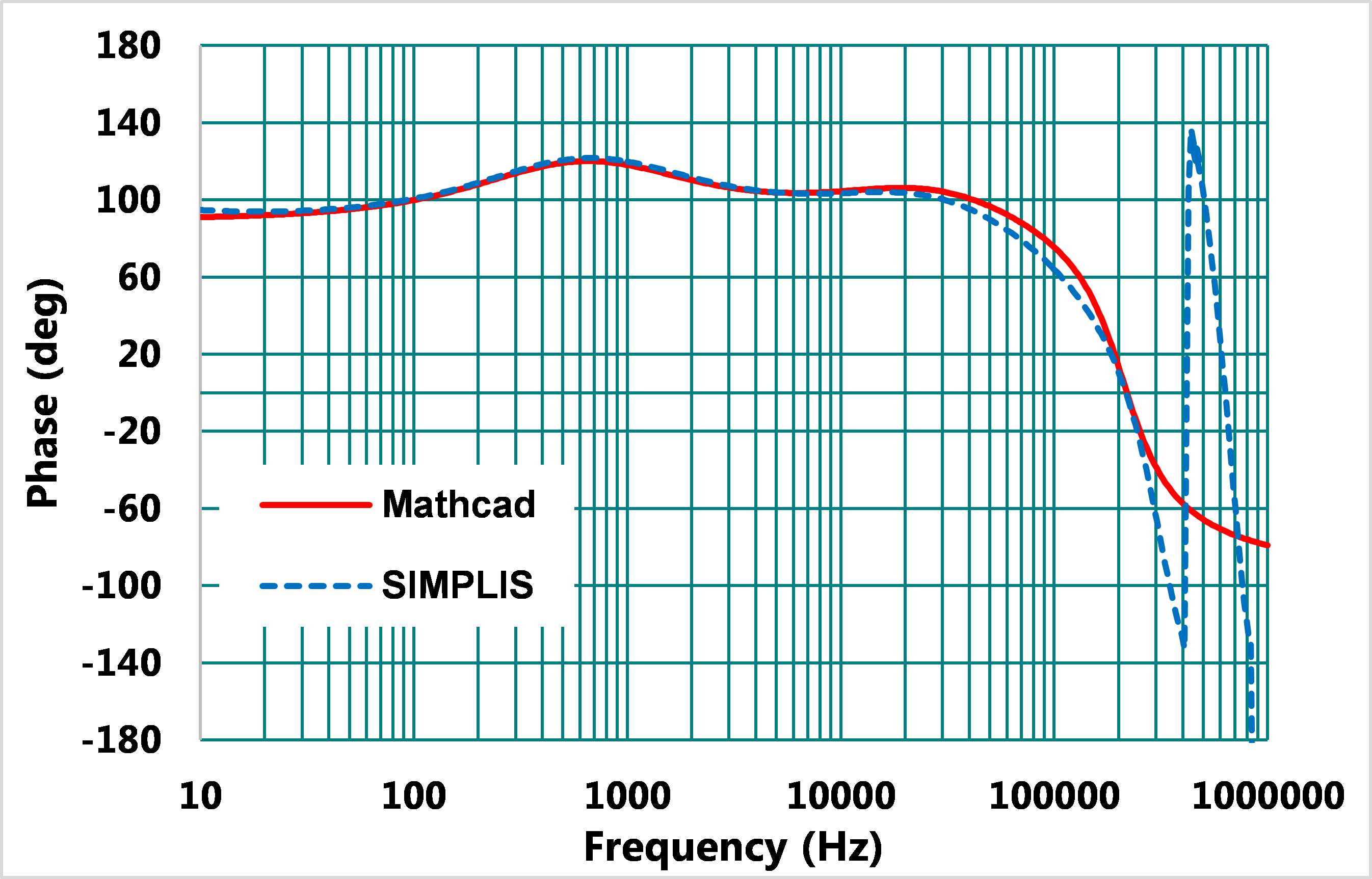
圖23、閉迴路相位曲線波德圖
上述之設計範例,維持相同的交越頻率,藉由加上相位提升的電容或電阻,可有效地提升相位與自由度。範例的設計參數與效益可參考下表。
|
Compensator Type
|
Type II
|
Type III
|
Type III
|
|
Extra components
|
N/A
|
Add CF1
|
Add CF1,RF3
|
|
fCZ1(Hz)
|
745
|
745
|
745
|
|
fCP1(Hz)
|
53.59 k
|
53.59 k
|
53.59 k
|
|
fCZ2(Hz)
|
N/A
|
20k
|
20 k
|
|
fCP2(Hz)
|
N/A
|
60 k
|
40 k
|
|
(CC1+ CC2)
|
12n
|
27.08n
|
28.374n
|
|
RF1(kΩ)
|
10
|
10
|
10
|
|
RF2(kΩ)
|
5
|
5
|
2.22
|
|
CC2(pF)
|
168
|
376
|
166
|
|
CC1(nF)
|
11.943
|
26.7
|
28.207
|
|
RC1(kΩ)
|
17.9
|
8
|
17.9
|
|
CF1(pF)
|
N/A
|
795
|
486
|
|
RF3(Ω)
|
N/A
|
N/A
|
6360
|
|
fC(Hz)
|
60k
|
60k
|
60k
|
|
Phase Margin
|
66°
|
92°
|
85°
|
四、結論
為了改善Type II補償器特性,獲得更好的相位提升,進而加強系統的穩定性,本文基於OTA Type II補償器架構,延伸出Type II 加相位提升電容以及Type II 加相位提升電容/電阻的Type III補償器;依序先分析工作特性與補償器理論,接著說明相位提升器的原理,並完整清楚的介紹元件參數設計概念;最後,用降壓型轉換器範例說明補償器的設計並加以驗證,若參考此設計方針進行補償器設計,有助於提升轉換器系統的穩定度。
五、參考文獻
[1] Raymond Ridley, “A New Small-signal Model for Current-Mode Control”, Ph.D. Dissertation, Electrical Engineering Department, Virginia Polytechnic Institute and State University, 1991.
[2] Jian Li, “Current-Mode Control: Modeling and its Digital application”, Ph.D. Dissertation, Electrical Engineering Department, Virginia Polytechnic Institute and State University, 2009.
[3] 王信雄博士, ”開關轉換器 控制理論與設計實務”